|
Probabilities
Theory
The six possible arrangements, or OUTCOMES, from the
simulation are summarized in the tree diagram in Figure 1.
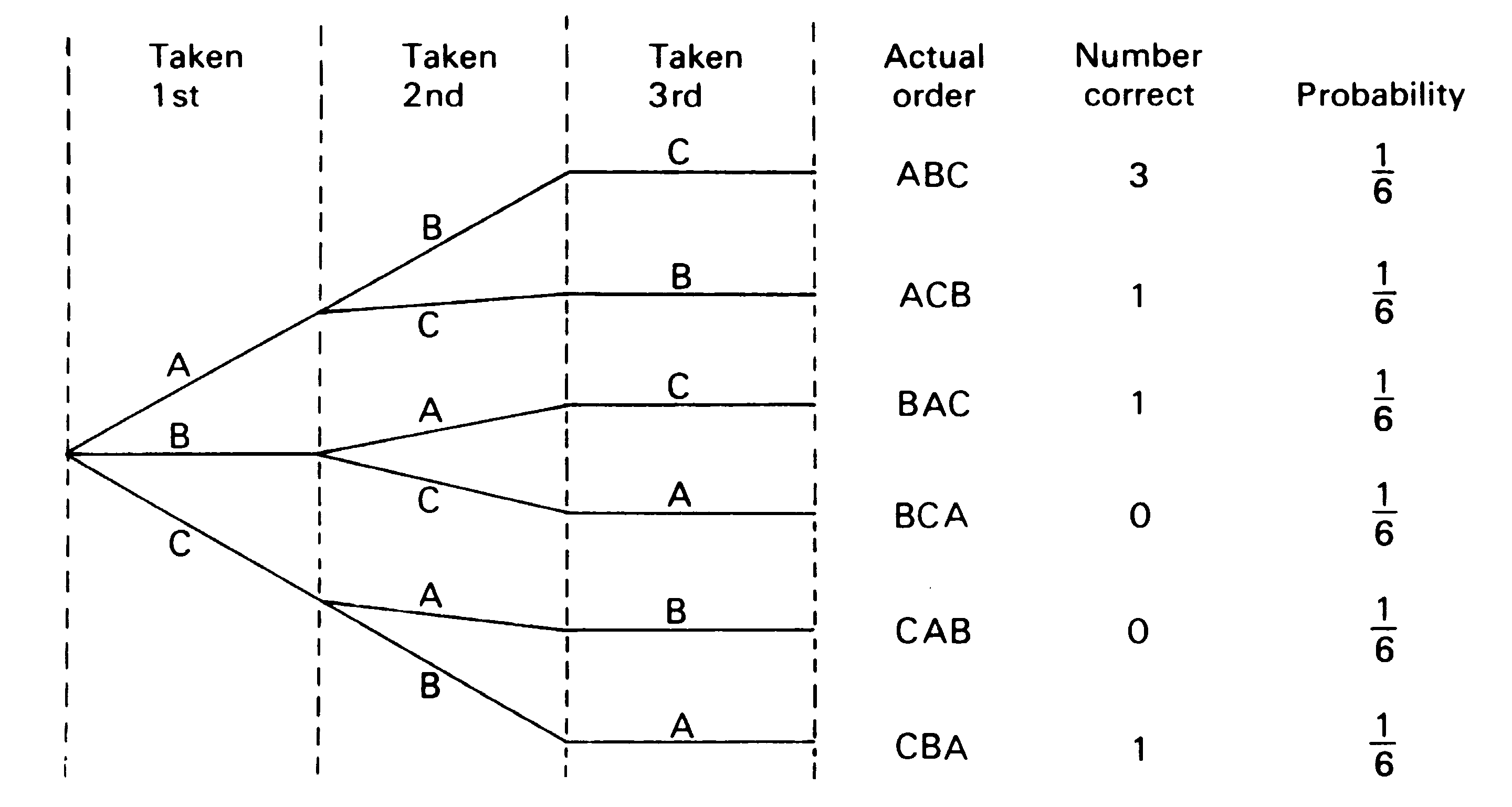
Figure 1 - Tree diagrams of possible outcomes.
Look carefully it the diagram and make sure you understand it.
The first person can choose from three.
The second person can choose from two.
The third person has the one left over.
- If you made you choices fairly in the simulation, do
you think any one outcome is more likely that any other?
If not. each outcome must be equally likely. There are Six
outcomes altogether. We expect each outcome to occur 1/6
of the time if done many times.
We write: Probability (ABC) = 1/6
Probability (ACB) = 1/6
- Write down two similar statements.
Other Probabilities
No-one receives the correct report when the outcome is BCA or
CAB.
So, if the simulation is done many times, we expect to get 0
correct on 1/6 + 1/6
= 2/6 of the times.
We write: Probability (0 correct) = 2/6
Use the tree diagram and a similar argument to find:
- Probability (1 correct)
- Probability (3 correct)
- Probability (2 correct)
Combining Probabilities
The tree diagram also provides information for other
probaibilities.
Suppose we want to find the probability of getting either 1 or
3 correct. This means getting ACB, CBA, BAC, or ABC.
There are four possible ways. The probability of each of these
four ways is 1/6.
In the long run we therefore expect to get 1 or 3 correct 4/6
of the times.
We write: Probability (either 1 or 3 correct) = 4/6
Use the tree diagram and similar reasoning to find:
- Probability (either 0 or 3 correct)
- Probability (either 0 or 1 correct)
- Probability (either 1 or 2 correct)
- Probability (0, 1 or 3 correct)
You found that it was never possible to get exactly 2 correct.
We say this is an impossible event and so:
Probability (2 correct) = 0.
Probability (4 correct) = 0 too.
- Why?
Getting 0, 1 or 3 right is certain to happen, so Probability
(0, 1 or 3 correct) = 1. You have worked out other probabilities
and in each case the answer was between 0 and 1.
- Copy the following:
All probabilities must be between or equal to 0 or 1.
An event which is impossible has probability 0.
An event which is certain has probability, 1.
The nearer a probability is to 1, the more likely the
event is to happen.
The nearer a probability is to 0, the less likely, the
event is to happen.
*Probability Connections
If we do not get 0 correct, we must get 1 or 3 correct, i.e.
at least 1 right. Notice that:
Probability (0 correct) = 2/6 and
Probability (at least 1 right) = 4/6 = 1 -
2/6
In this example:
Probability (at least 1 right) is 1 - Probability (0 correct).
Use Your answers to C2 and C3 to find the connection
between:
- Probability (3 correct) and Probability (no more
than 1 correct).
- Probability (1 correct) and the probability of
being right or totally wrong.
Proportions and Probabilities
Look again at Table 6.
Write down two answers for each of the following, the
first answer for your own results, the second for the class
results.
- Proportion of outcomes which give all correct.
- Proportion of outcomes which give 0 correct.
- Proportion of outcomes which give 1 correct.
- Proportion of outcomes which give 0 or 3 correct.
We have already found the corresponding probabilities for
these outcomes. They are:
Probability (all correct) 1/6 ( = 0.17)
Probability (0 correct) = 2/6 (= 0.33)
Probability (1 correct) 3/6 (= 0.5)
Probability (either 0 or 3 correct) = 3/6
( = 0. 5)
- Compare the proportions from your results with
these probabilities. Write a sentence describing what you
find.
- Compare the proportions from the class results
with these probabilities. Write a sentence describing
what you find.
- Write a sentence to explain any differences or
similarities that you may have found in your answers to e
and f.

The Coffee Problem
Let us see how the theory applies to the coffee competition
mentioned in Section A. The coffees are given in the order
Brazilian, Kenyan and Continental.
- What is the chance that a person identifies the
three coffees correctly?
- To find out, complete the tree diagram F'igure 3
on page R1. The first branches of the tree are done for
you.
- The correct order is B K C; complete the column
headed '
Number correct'.
Complete the column headed 'Probabilities'.
You should have said that the probabilities in each case were 1/6
and found that the completed tree diagram looked rather like the
tree diagram in Figure 1.
- What is the probability that one person gets them
all in the right order?
Suppose you were organizing the competition and expected 100
people to enter.
- How many prizes would you expect to provide?
- Would you change this number if you knew the
coffees tasted very different? Explain your answer.
*Multiple Choice
A multiple choice question on a history, paper asked
candidates to arrange the battles of Verdun, Marne and the second
battle of Ypres in date order, starting with the earliest.
John knows no history, but decides to guess.
- What is the chance that he will get full marks?
- To find out, draw and complete an outline tree
diagram similar to the one started in Figure 3 on page
R1.
- Using the letters M, Y, V, complete the tree
diagram to show all the possible outcomes.
- If the correct order is MYV, complete the column
headed '
Number correct'.
Complete the column headed 'Probabilities'
What is the probability that John gets them all in the
right order?
Suppose a class of 30 pupils all guessed.. How
many would you expect to get full marks?
*Suppose the class all guessed and marks are
given +4 for a battle in the right position and 1 for a
battle in the wrong position. This would mean that a
pupil writing VYM would earn - 1 + 4 - 1 = +2. What are
the possible marks? You may find it helpful to add an
extra column headed 'Marks obtained' at the end of the
tree diagram.
*How many people would you expect to get each
possible mark?
|