Brief Description
Aims and
Objectives
Prerequisites
Equipment
and Planning
Section A
- What's What
Section B
- The Effects of Chance
Section C
- Probabilities
Section D
- Taste Testing
Section E
- More People
AnswersResources
Test
Questions
Test
Questions - Answers
Connections
with Other Units
|
 |
Brief Description
Pupils investigate the effects of chance in a variety of situations, and are asked to
question the meaning and validity of advertising claims.
Design time: 3-4 hours
Aims and
Objectives
By the end of Section C pupils should be able to list all possible outcomes
for a simple experiment, assign probabilities when these outcomes are equally likely, and
add these simple probabilities to obtain the probabilities of compound events. They will
have practised tallying, completing tables, calculating proportions and completing tree
diagrams. They will be more aware of some of the problems in designing experiments, the
effect of chance, the connection between relative frequency of success and probability,
and that probabilities lie between 0 and 1.
Those who finish the complete unit will also be able to assign probabilities from
counting the equally likely events on a tree diagram. They will have practised combining
probabilities of mutually exclusive events, calculating binomial coefficients and applying
them to finding the probabilities of obtaining 2 successes out of 4 and 8 successes out of
10 when the probability of a success is 1/2. They will be more aware
of the properties of the binomial distribution and of how probabilities can be linked with
such statements as "8 out of 10 cats prefer Whiskas".
Prerequisites
Pupils need to be able to (i) convert fractions into decimal fractions in Section B
(using a calculator if available) and (ii) recognize Pascal's triangle in the optional E1.
Equipment
and Planning
The unit can be used in two ways:
- As a complete whole, requiring a copy of pages R1 and R2 for each pupil;
- In two stages:
- Sections A, B, C, which require a copy of page R1 for each
pupil.
- Sections A1, D, E, which require a copy of page R2 for each
pupil.
If, however, pupils are already familiar with probability and tree diagrams, then it is
possible to omit Sections A2, B, C. If time and ability permit,
all the tree diagrams and tables could be drawn by the pupils instead of using R pages.
The simulation in B1 requires the class to be divided into groups of four,
although if the class is small, they can work in threes, or even individually.
Each group requires three identical pieces of paper or carefully cut card, one of each
marked A, B or C. Sections C and D can be
done individually, although discussion of possible outcomes is to be encouraged.
C6 can be short-circuited by more able pupils, by moving directly from the
discussion question to questions f and g.
C7 is optional reinforcement, while other asterisked sections or questions are
for more able pupils. They can be omitted without destroying the thread of the unit.
Detailed
Notes
Section A
A1
This introduces pupils to the possible ways of interpreting statements apparently
based on statistical trials. Class discussion may help here.
- Pupils should be encouraged to think of other rneanings. Their own interpretation should
be recorded as they will refer back to it later.
- Pupils should appreciate that the cat may not distinguish between the cat foods. Some
comments may reflect a mistrust of advertising claims in general. This could usefully be
followed up by a discussion of the IBA Code of Advertising Standards and Practice, copies
of which are obtainable free from the Independent Broadcasting Authority, 70 Brompton
Road, London, SW3 IEY
A2
Here it is unlikely that the 100 people would all be coffee experts. Discussion
could usefully include:
- the likely effect of bias if the competition were held in a shop renowned for its choice
of coffee beans, compared with a stand in a supermarket.
- such possibilities as 80 people getting it right or 20 people getting it right.
- If the coffees tasted the same, then the competitors would beaware that they were 'just
guessing'. Getting the right answer is just a matter of luck.
- If the coffees tasted different, then the competitors would not necessarily be prepared
to admit they were guessing. Nevertheless, unless the competitors were regular coffee
drinkers it is unlikely that many would have the skill to distinguish the tastes
correctly.
Section B
B1
This will require a copy of page R1 for each pupil.
The simulation should produce a reasonable distribution of possible outcomes. It is
necessary to stress the need to shuffle the papers, to fold them in the same way and to
select without looking.
Some ability groups may find this experiment more interesting if a financial element is
introduced at the end. For example, you can suggest a prize of 20p if all three letters
are in the correct envelopes, 5p if one only is in the correct envelope and a penalty of
10p if all the letters are incorrectly addressed. These amounts can then be applied to the
successes actually achieved and the outcomes in the tree diagrams to see the actual and
expected profit to be made. Table T1 shows the profit for each of the six outcomes.
| Outcome |
No. correct |
Profit |
| A B C |
3 |
20p |
| A C B |
1 |
5p |
| B A C |
1 |
5p |
| B C A |
0 |
-10p |
| C A B |
0 |
-10p |
| C B A |
1 |
5p |
| Total profit (6 outcomes) 15p |
Table T1 - Profit on putting letters in envelopes
So on six outcomes we should expect a profit of 15p, i.e. an expected profit of 21/2p
per experiment.
B2
Some help may be required with transfer of results from Table 5 to Table 6.
- - c. Tally marks could be used to assist this process.
- Some mention of "If two right, then the third one must be" is
required.
- Calculators might help here.
- This is probably best done by the teacher writing the results on the blackboard to
obtain totals for each outcome, and then pupils entering them in Table 6. Invite comments
from pupils on proportions obtained. This links later with C5. Look for
tendencies to stability as the number of trials is increased.
B3
- In only 15 trials it is possible that all six arrangements may not occur. If very few of
the arrangements occur, then this raises questions about the way the group did the
simulation. This may provide a useful reminder of the need to ensure standard practices in
any simulation.
Section C
The link is made here to the theoretical situation, and the tendency of the
proportions, in the long run, to approximate to the theoretical probabilities. The
introduction is made by means of tree diagrams.
C3
Pupils are asked to copy the summary for completeness, but this could be omitted.
Illustration by means of points on a probability number line, as shown here, may help.
C5
Notice the need for addition of proportions in d. It might help
to draw an outline table on the blackboard for pupils to copy and fill in their own
proportions, for example:
| Outcome |
Group proportions |
Class proportions |
Probability |
| ABC |
0. |
0. |
0.17 |
| 0 correct |
0. |
0. |
0.33 |
| 1 correct |
0. |
0. |
0.5 |
| 0 or 3 correct |
0. |
0. |
0.5 |
It is expected that the class proportions will be much nearer the probabilities than
the group proportions.
C6
If confident and accurate replies are given to the discussion question, move
directly to f and g.
*C7
Optional reinforcement.
- Some pupils may need help here. Intuitively some will probably say 5, but if the ability
of the class is high it would be advantageous to show that 5 is the most likely outcome
when the probability of success is 1/6.
Section D
In this section pupils extend the application of tree diagrams from two people to three
and four people.
The probability of success used is 1/2 to ease the calculation.
Stress throughout that results are obtained by guessing. i.e. by chance.
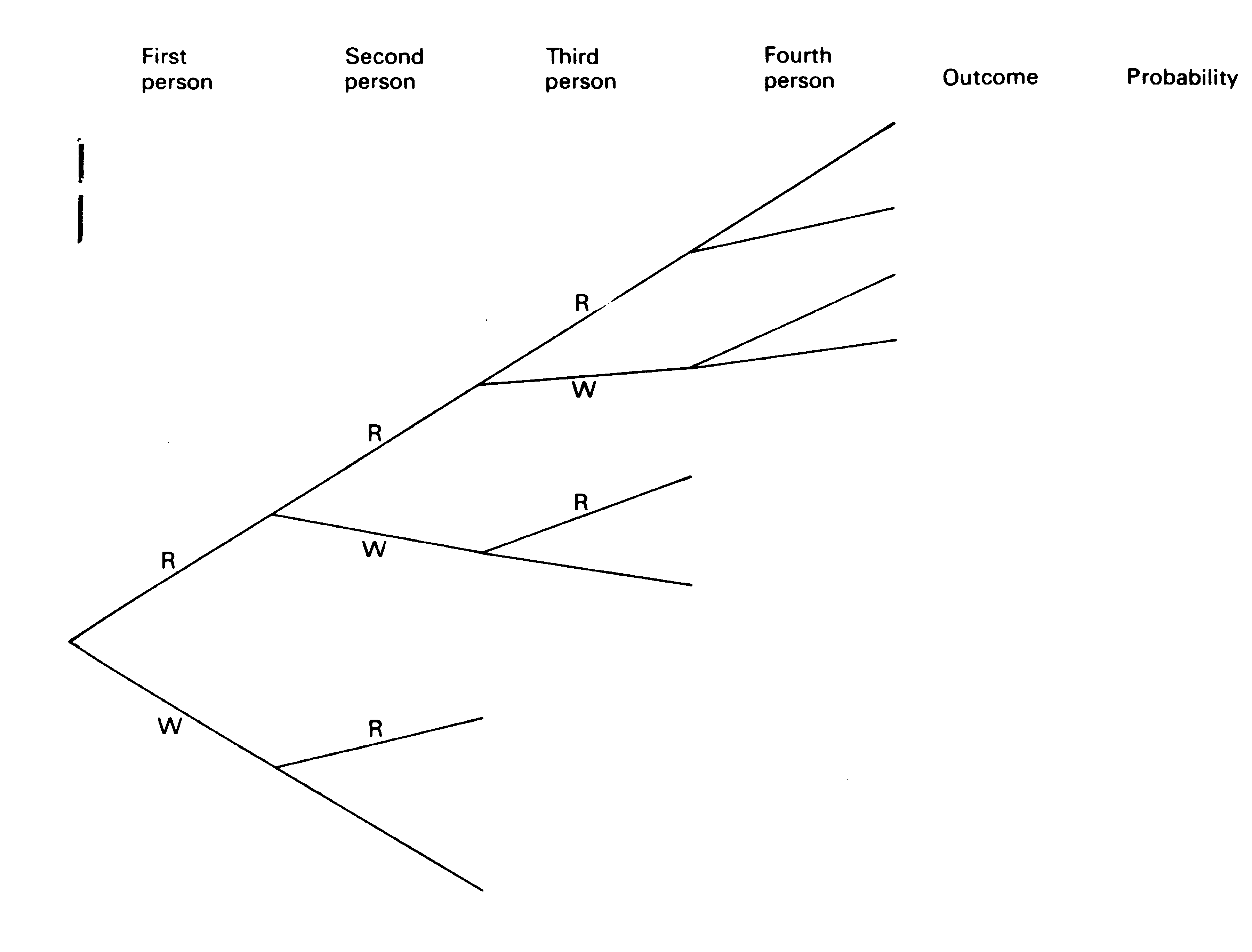
D2
Figure 4 and Table 7 can be copied and completed if this is preferred.
D3
- Probabilities are not the same.
- Make certain that their answer here is compared with their guess in a.
Probability (1 out of 2 guess correctly) = 1/2 = 0.5
Probability (2 out of 4 guess correctly) = (6 x 1)/16 = 3/8
= 0.375
Section E
This extends the idea of chance to the 8 out of 10 situation.
*E1
This section is optional and is for more able pupils. Table 4 is another way of
looking at Pascal's triangle, and shows the number of possible ways of getting different
numbers of successes in different cases. Pupils may need help to complete the table, which
could be drawn up and completed on the blackboard if preferred. k and l
are for those pupils who have done C4.
E2b
It is important that the result should be obtained if at all possible, perhaps as
a class exercise, and with the use of a calculator. It is still intended that Probability
(success) = 1/2. If the result is not obtained, it will have to be
given to the class for E3.
E3
Probability of 8 out of 10 getting it right is:
45/210 = 0.044 (or 56/210
if 'at least 8' out of 10)
If, therefore, the test on cat food was carried out as a standard statistical
experiment, the probability that 8 out of 10 get it right by chance is not very high. The
question is whether it was a standard statistical experiment.
- Encourage any interpretation which shows the pupil is aware of the effect of chance on
such results and the questionable nature of the statistical evidence sometimes used to
support advertising claims.
*E4
This also is an optional section. It raises the question of the effect of
changing the probability of success. It is left to the teacher to extend the ideas still
further if required. Reference can usefully be made to How to Lie with Statistics
by D. Huff (Penguin, 1973).
Answers
C2
- Outcomes ACB, BAC, CBA; Probability 1/6
+ 1/6 + 1/6 = 3/6
- Outcome ABC; Probability 1/6
- Impossible; Probability 0
C3
- Outcomes BCA, CAB, ABC; Probability 1/6
+ 1/6 + 1/6 = 3/6
- Outcomes ACB, BAC, BCA, CAB, CBA;
Probability 1/6 + 1/6 + 1/6
+ 1/6 + 1/6 + = 5/6
- Outcome ACB, BAC, CBA; Probability 1/6
+ 1/6 + 1/6 = 3/6
- All possible outcomes; Probability 6/6 = 1
- Impossible with only three reports
C4
- 1 - Probability (3 correct) = Probability (no more than 1 correct) = 5/6
- 1 - Probability (1 correct) = Probability of being completely right or totally wrong =
Probability (0 or 3 correct) = 3/6
C6
- 1/6
- 100/6 = 17 on chance alone, if coffees tasted much the
same
- Likely that more people will get it right since some may be able to distinguish at least
one from the other two, reducing the effects of chance.
C7
- +12, +2, 3
- 5 score + 12, 15 score + 2, 10 score -3
D1
- 1/4
- 1/4
- 1/2
D2
- 1/8
- 3/8
- 3/8
- 1/8
D3
- 1/16
- 1/4
- 6/16
- 2
- No
- 1 - 1/16 = 15/16
- 11/16
E1
- 1/32
- 5/32
- 2 or 3 have equal probabilities of 10/32
- 31/32
- 26/32
E2
- 45/210 = 0.044
E4
- 1/6
- Probability (2 right out of 4) = 6 x (5/6)2
x (1/6)2 = 0.12
Probability (1 right out of 2) = 2 x 5/6 x 1/6
= 0.28
Test
Questions
- Three cards, a Jack, a Queen and a King, are shuffled and then turned up one at a time.
- Copy and complete Figure 1 to show the possible outcomes.
- Fill in the column headed 'Probability'.
Find:
- Probability (order is JQK)
- Probability (the second card is a King)
- If the experiment were done 100 times, about how often would you expect the Jack to be
the first card?
Figure 1 - Tree diagram showing results from three cards
- Write down the probability of
- an impossible event,
- a certain event,
Using the possible outcomes from the three cards in question 1, give an example of:
- an impossible event,
- a certain event.
- A person is given a piece of cheese. He is told it is either English cheddar or New
Zealand cheddar, and is asked to say which.
- If he just guesses, what is the probability he will be right?
Three people are asked to do the cheese test. Suppose they all guess. The possible
outcomes can be shown in a tree diagram.
- Copy and complete Figure 2 to show the possible outcomes.
Figure 2 - Tree diagram for three people trying the cheese test
- Fill in the column headed 'Probability'.
Suppose it was English cheddar. Find:
- Probability (all 3 right)
- Probability (exactly 1 right)
- Probability (all wrong)
- Probability (exactly 2 right)
- Probability (at least 1 right)
- You are not expected to draw a tree diagram or do any calculations to answer this
question.
Suppose six people were asked to do the cheese test and they all guessed
- What is the most likely number that would get it right?
- Is the Probability (2 right out of 6) the same, more than, or less than Probability (1
right out of 3)?
Answers
-
-
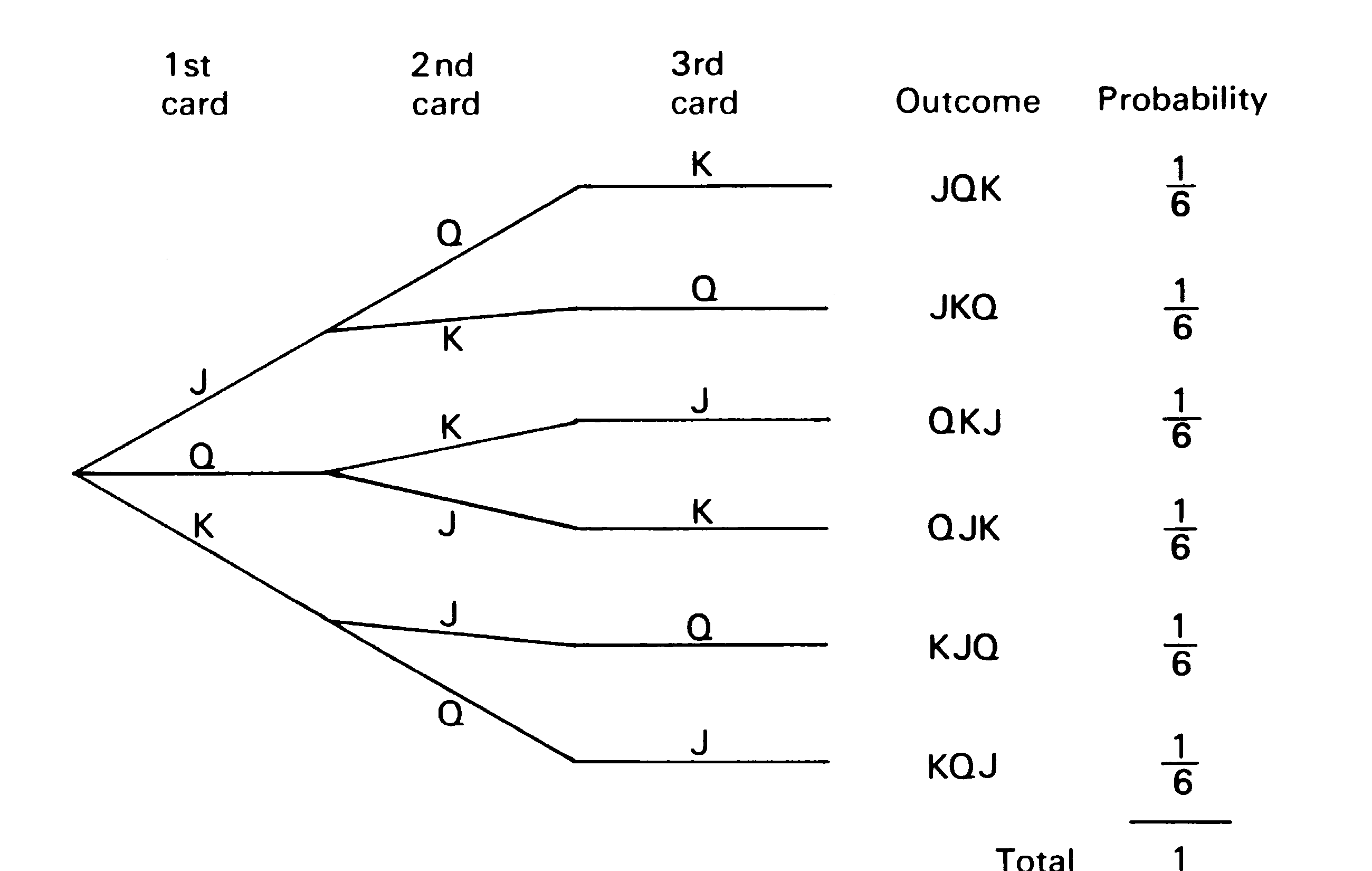
Figure 1- Probability (order is JQK) = 1/6
- Probability (the second card is a king) = 2/6
- Probability (1st card is a Jack) = 2/6
In 100 trials, expected number = 100 x 2/6 = 33
-
- Probability (impossible event) = 0
- Probability (a certain event) = 1
Various possibilities exist for c and d; some
suggestions are listed here:
- Probability (of getting an ace)
Probability (not a court card)
Probability (exactly 2 out of 3 in correct order of JQK)
- Probability (outcome contains a Jack, Queen and a King)
Probability (three different cards)
Probability (obtaining three court cards)
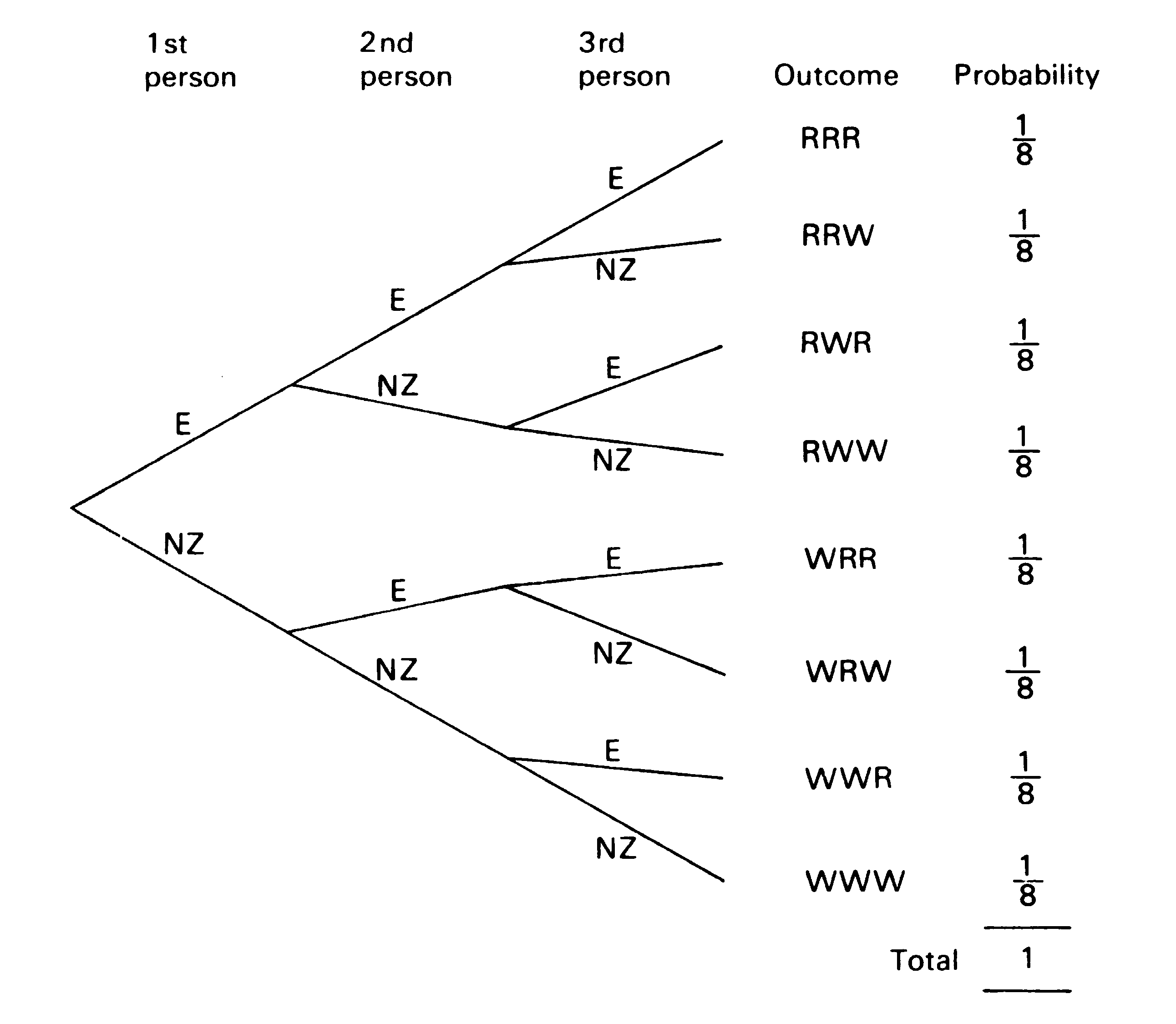
Figure 2
- Probability (all three right) = 1/8
- Probability (exactly 1 right) = 3/8
- Probability (all wrong) = 1/8
- Probability (exactly 2 right) = 3/8
- Probability (at least I right) = 7/8
-
- 3
- Less than; Probability (1 right out of 3) = 3/8
Probability (2 right out of 6) = 15/64
but pupils are not expected to work this out
Resource Pages
Figure 3
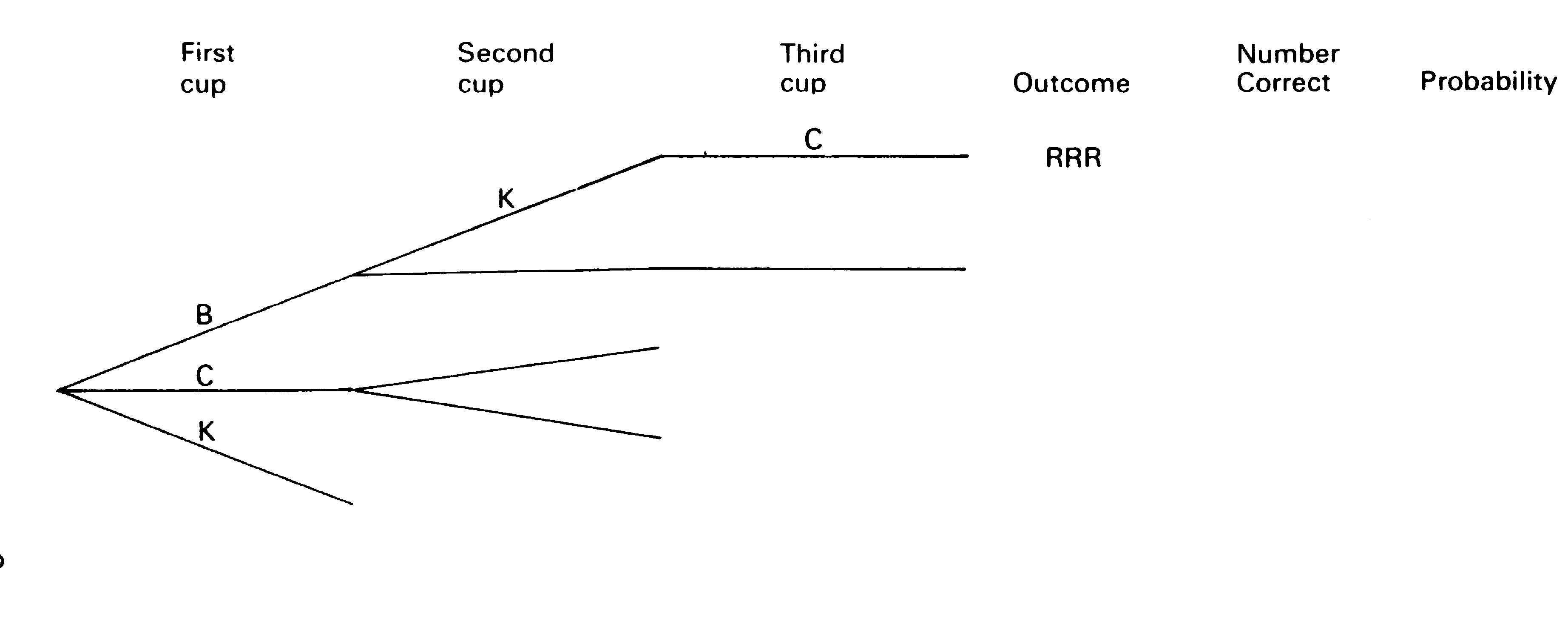
Figure 4
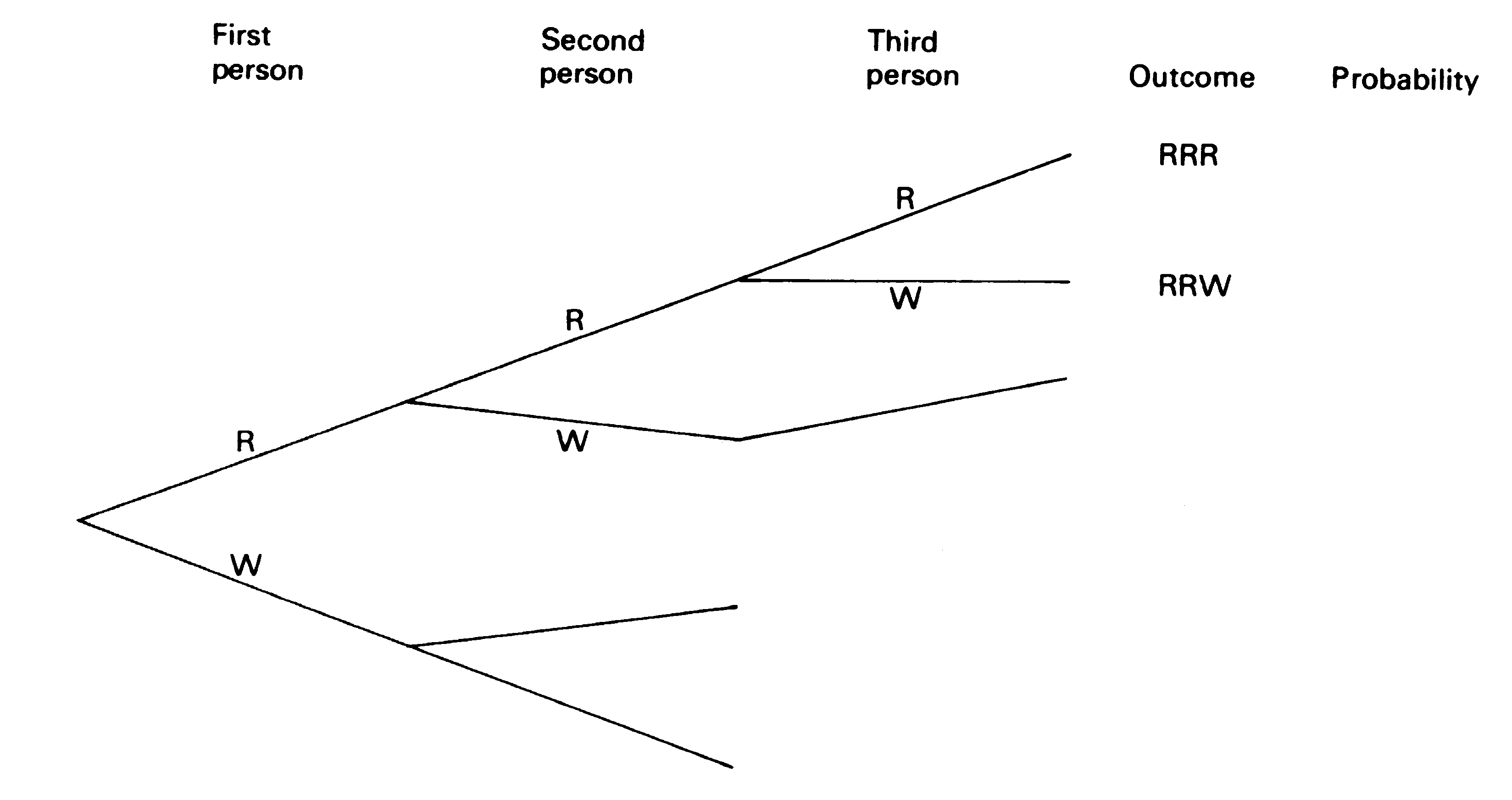
Figure 5
Connections
with Other Published Units from the Project
Other Units
at the Same Level (Level 4)
Figuring the Future
Sampling the Census
Testing Testing
Retail Price Index
Smoking and Health
Equal Pay
Units at
Other Levels In the Same or Allied Areas of the Curriculum
Level 1
Shaking a Six
Being Fair to Ernie
Probability Games
If at first...
Level 2
On the Ball
Fair Play
This unit is particularly relevant to: Mathematics.
Interconnections
between Concepts and Techniques Used In these Units
These are detailed in the following table. The code number in the left-hand column
refers to the items spelled out in more detail in Chapter 5 of Teaching Statistics
11-16.
An item mentioned under Statistical Prerequisites needs to be covered before
this unit is taught. Units which introduce this idea or technique are listed alongside.
An item mentioned under Idea or Technique Used is not specifically introduced
or necessarily pointed out as such in the unit. There may be one or more specific examples
of a more general concept. No previous experience is necessary with these items before
teaching the unit, but more practice can be obtained before or afterwards by using the
other units listed in the two columns alongside.
An item mentioned under Idea or Technique Introduced occurs specifically in
the unit and, if a technique, there will be specific detailed instruction for carrying it
out. Further practice and reinforcement can be carried out by using the other units listed
alongside.
| Code No. |
Statistical Prerequisites |
|
|
| |
None |
|
|
| |
Idea or Technique Used |
Introduced in |
Also Used in |
| 1.3e |
Variability in samples |
Being Fair to Ernie
Probability Games
If at first...
Fair Play |
On the Ball
Smoking and Health |
| 2.1a |
Constructing single variable frequency tables |
If at first... |
Being Fair to Ernie
Retail Price Index
Figuring the Future |
| 4.2b |
Probability of mutually exclusive events |
|
|
| 4.3d |
Binomial model p = 1/2, small n |
|
|
| |
Idea or Technique Introduced |
Also Used in |
| 4.1a |
Relative frequency of success |
Shaking a Six
Probability Games
Testing Testing |
| 4.1c |
Equally likely probabilities as expected relative frequencies |
Shaking a Six
Testing Testing
Probability Games
On the Ball |
| 4.1e |
Probability of single sample from known population |
Probability Games
On the Ball
Testing Testing |
| 4.1i |
Elementary events |
|
| 4.1j |
Assigning probabilities to events |
Testing Testing |
| 4.1m |
Fairness and equally likely probabilities |
Probability Games
If at first...
Fair Play |
| 4.1o |
Systematic counting of outcomes |
Probability Games
Fair Play
Testing Testing |
| 4.3o |
Simulation as a model |
Testing Testing |
| 4.3p |
Setting up a simuiation |
If at first...
On the Ball
Testing Testing |
| 4.3q |
Interpreting a simulation |
If at first...
On the Ball
Testing Testing |
| 5l |
Elements of design of experiments |
|
| 5x |
Comparing actual with expected values |
Being Fair to Ernie
On the Ball
Testing Testing
Probability Games
Fair Play
If at first...
Figuring the Future |
|