Other Probabilities

What Does a Positive Reaction Mean?
Look back at Table 1.

1. How many drivers gave a positive reaction?
2. Of these, how many were drunk?
3. Of those who gave a negative reaction, how many were drunk?

It is possible to draw a different tree diagram from the information contained in the table.

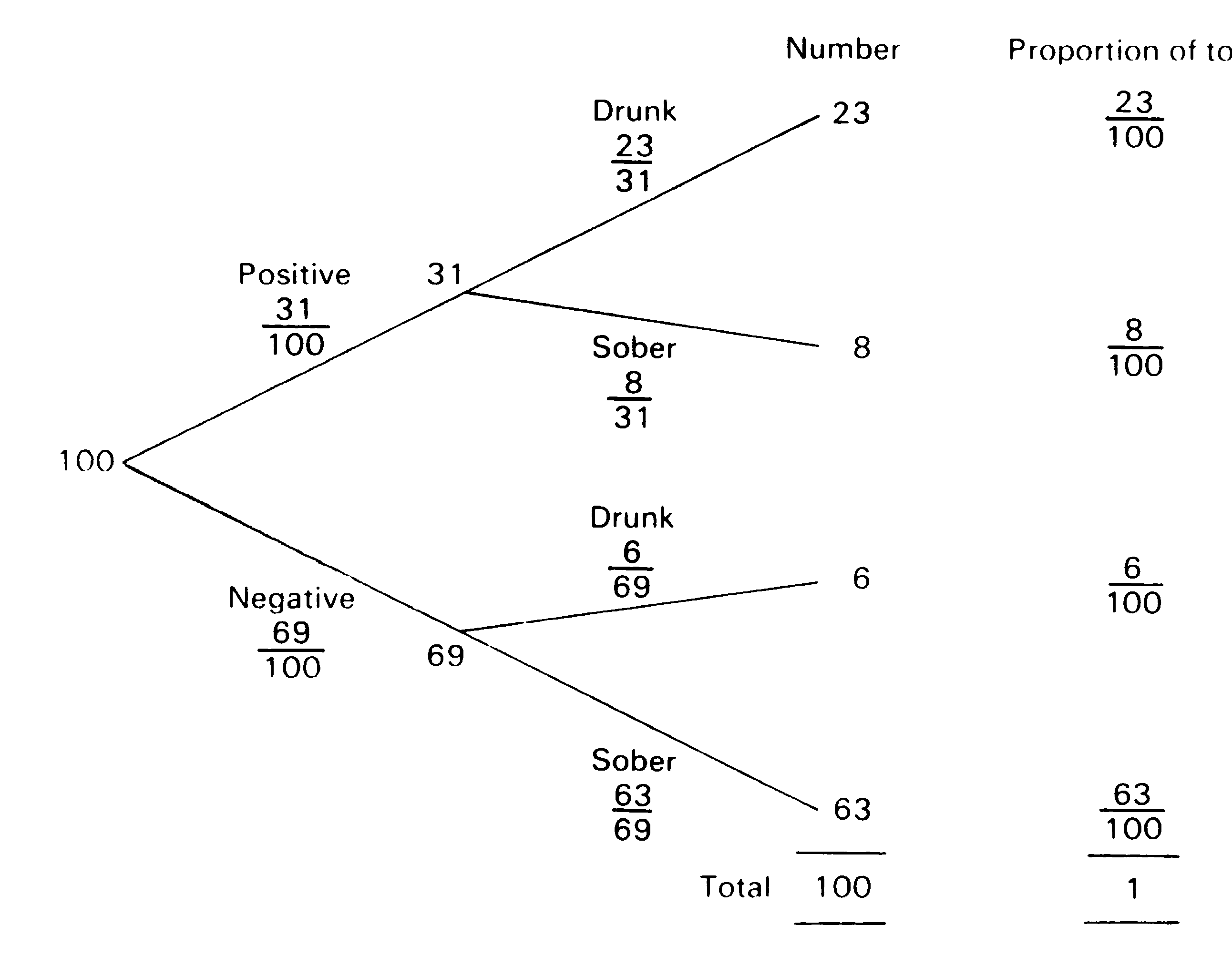
Figure 2 - Tree diagram showiong further results from Table 1.

Using Figure 2, estimate the following:

4. Probability (a driver who gives a positive reaction is sober)
5. Probability (a driver who gives a positivereaction is drunk)
6. Probability (a driver who gives a negative reaction is drunk)
7. Probability (a driver who gives a negative reaction is sober)
8. Probability (a driver is both drunk and gives a positive reaction)
9. Probability (a driver is both sober and gives a positive reaction)
10. Probability (a driver gives a positive reaction)
11. *Can you find a relationship between some of the answers to d to j. If so, write it down first as a multiplication sum involving fractions and then in words, using probabilities.
12. Make a copy of Figure 2, but insert the figures obtained from your version of Table 1.
13. Work out the proportions based on your figures and insert them in the boxes.
14. Use your tree diagram to find the answers to d to j from your simulation.

Practice Makes Perfect - or Does It?
When the breathalyser is administered by a policeman and the driver reacts negatively, he will not be asked to give a blood sample.

It will never be known whether he was drunk and the breathalyser was at fault, or whether he was really sober.

1. Which of the two tree diagrams, Figure 1 or Figure 2, best represents this situation?
2. How much of the tree diagram would it be possible to complete?
3. Which error will be identified?
4. Which is the most important error? Why?

It is obviously important to make the number of errors as small as possible.

5. How can this best be done?

*Connecting Probabilities
Look back at your answers to B5g and C1k. They have a lot in common, but do not say the same thing. Can you find any connection between them?

Querying the Assumptions
Do you think that the assumptions In Section B2 were realistic? Discuss this and make other, more realistic suggestions.

1. Use these suggestions to draw and complete a tree diagram like Figure 1. You may find it helpful to assume that 1000 people were tested.
2. Use your new tree diagram to estimate the probabilities required in B5.

Should Random Breath Tests Be Allowed?
We have looked at possible results, assuming that the police are allowed to use random breath tests. We have seen that errors can occur, that innocent people can appear to be drunk, and gullty people can appear to be sober. We know that these same mistakes will occur whenever the breathalyser is used, whether it is used randomly or not.

How then shall we decide whether or not to use random testing?

We need to consider the alternative, which we will call selective testing, as It exists at the moment.

Remember that at the present time the policeman is more likely to pick on a drunken motorist to test than if he chooses whom to test strictly at random. But unless the driver has done something wrong, or has a light not working, at present the policeman cannot stop him.

So there are likely to be many drunken motorists who do not get stopped. What we need to consider is the number of errors that occur now and compare it with the errors likely if random tests were used.

We also need to consider how manv more drunken motorists would be caught if random tests were allowed.

Which is better, random testing or selective testing? You will need to make some more assumptions and discuss this with your teacher before you have enough evidence to come to any conclusion.

1. Write down anything you need to know before you can come to a decision.
2. Compare answers with other members of the class and see if you can decide which is better, random testing or selective testing.
3. Write a statement when you have decided and give your reasons.

 

Back