| 
Looking at
Errors
Testing the
Breathalyser
Before the breathalyser was adopted for use by the police its efficiency was tested
against the totally reliable blood test.
Suppose a group of 100 drivers were asked to help test the efficiency, of the
breathalyser by taking both the breathalyser and the blood tests.
We could then get a set of results like Table 1.
| |
Positive |
Negative |
Total |
| Drunk |
23 |
6 |
29 |
| Sober |
8 |
63 |
71 |
| Total |
31 |
69 |
100 |
Table 1 - Results of 100 tests of the breathalyser.
Use the table to answer the following questions:
- How many drunk drivers were there altogether?
- How many of the 100 people gave a positive reaction?
Now look at the numbers that go to make up the totals.
- How many drunk drivers gave a positive reaction?
- How many sober drivers gave a negative reaction?
If the breathalysers were totally reliable. these two answers would include all the
drivers tested. i.e. they would total to 100, and the other two numbers would be 0.
The breathalyser is not completely reliable. It can make errors. People who are drunk
can get a negative reaction from the breathalyser.
- How many drunk people did not react (i.e. gave a negative reaction)?
What would happen to these people if they had been stopped by the police?
People who are sober can get a positive reaction from the breathalyser.
- How many sober people reacted positively to the breathalyser?
What would happen to these people if they had been stopped by the police?
We have seen that two types of error are possible. One is that a drunk person does not
react to the breathalyser and is regarded as sober.
- Write down the other type of error.
100 Random
Tests
Suppose the police decide to test the breathalyser on a random sample of motorists. They
stop 100 motorists, ask them to use the breathalyser and then check their results using a
blood test. You can simulate the possible results.
Assume the following:
30% of the motorists on the road at this time are drunk.
80% of the drunken motorists stopped give a positive reaction.
10% of the sober motorists stopped give (incorrectly) a positive reaction.
You need a table of two-figure random numbers. Your teacher will tell you how to use
them.
If the first digit of the pair is 0, 1 or 2, the driver is drunk.
If the driver is drunk and the second digit is 0, 1, 2, 3, 4, 5, 6, 7, then he reacts
positively
If the driver is sober and the second digit is 0, then he reacts positively.
These rules are summarized in the following table:
Drunk and
positive |
00 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
| 10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
|
| 08 |
09 |
Drunk and
negative |
| 18 |
19 |
| 28 |
29 |
|
Sober and
positive |
30 |
| 40 |
| 50 |
| 60 |
| 70 |
| 80 |
| 90 |
|
| 31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
Sober and
negative |
| 41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
| 51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
| 61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
| 71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
| 81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
| 91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
|
Table 2 - Using the random numbers.
If the results in Table 1 had been obtained from a simulation,
they would have originally been recorded as In Table 3.
| |
Positive (+ve) |
Negative (-ve) |
| Drunk |
    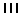 |
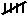  |
| Sober |
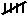 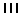 |
             |
Table 3 - Results of simulation.
- Draw a blank table like Table 3. Read off 100 two- figure random
numbers, and record your results on your table.
- Draw a blank table like Table 1 and use it to record the final
figures from your simulations.
Use your results to answer the following questions:
- How many drunk drivers were there altogether?
- How many of the 100 people gave a positive reaction?
- How many drunk people gave a negative reaction to the breathalyser?
What would happen to these people if the breathalyser alone had been used?
- How many sober people reacted positively to the breathalyser?
What would happen to these people?
- How do your results compare with the results in Table 1? Are more errors made? Write a
sentence to describe what you find.
Proportions
Much as everyone would like the breathalyser to work to be prepared for perfectly, it
doesn't, so we have to be prepared for 'unfair' results from it. Whether we collected 10
results or 1000 results, there could still be errors. What is important is the Proportion
of errors.
Table 1 shows that the proportion who were both drunk and reacted positively is 23/100
Use Table 1 to find:
- The proportion of people who were both sober and reacted positively.
- The proportion of people who were both drunk and reacted negatively.
Suppose we consider only those who were drunk.
There were 29 of these.
23 of these 29 gave a positive reaction.
Therefore, we say the proportion of drunk drivers who gave a positive reaction, i.e.
did react, is 23/29.
Use Table 1 to answer the following:
- Of the 29 who were drunk, how many gave a negative reaction, i.e. did not react? What
proportion of the drunk drivers is this?
- How many were sober? Of these, how many did react? What proportion of the sober drivers
did react?
- What proportion of the sober drivers did not react?
- Now answer questions a to e using the results you obtained from your simulation.

Tree
Diagrams
The information in Table 1 and the proportions we have just found
can be summarized in a tree diagram.
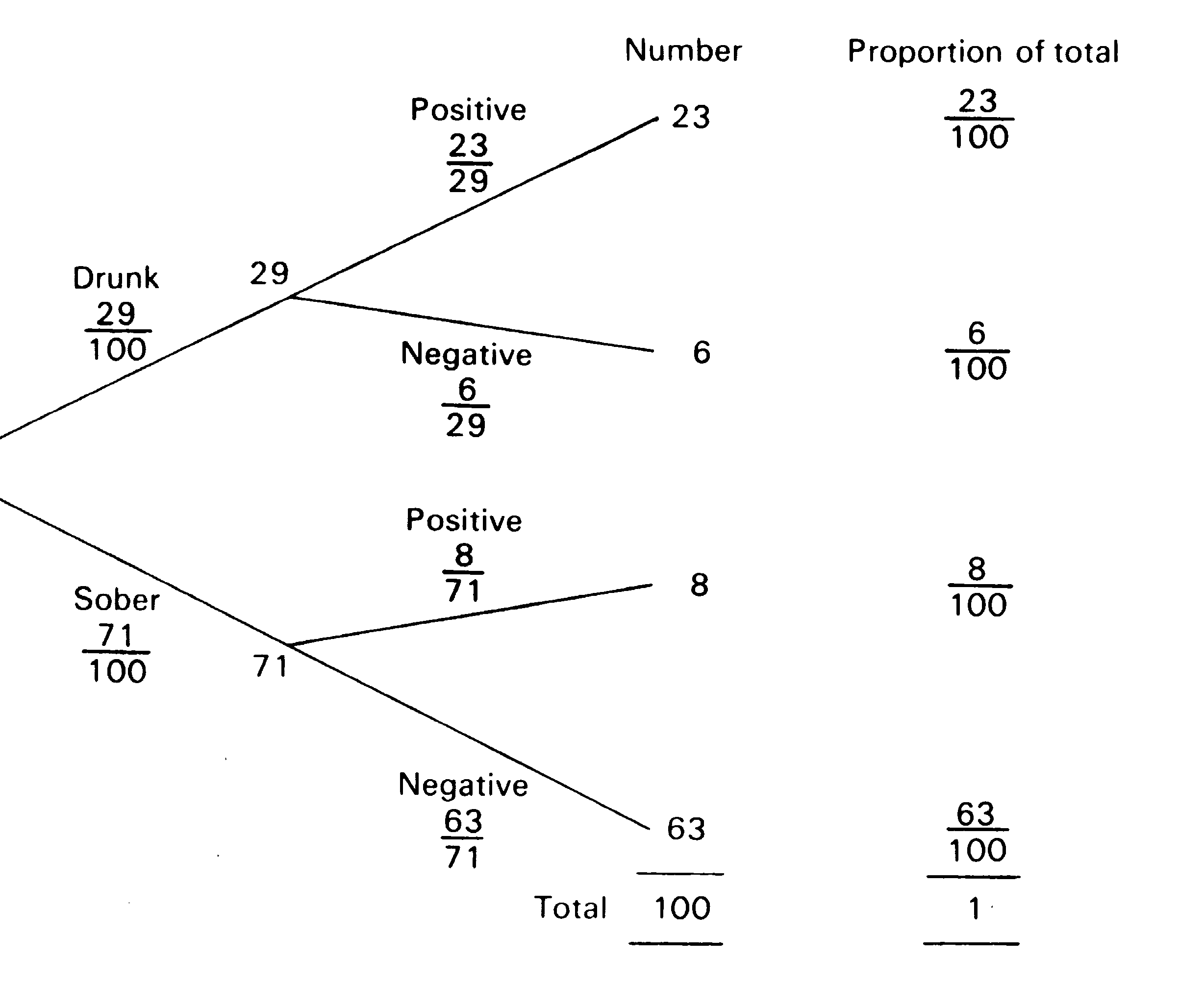
Figure 1 - Tree showing proportions obtained from Table 1.
- Make a copy of the tree diagram, but in the boxes put the proportions obtained
from your simulation. Some of these will be the answers you gave to B2f.
Others you will have to work out for yourself.
- Complete the column headed 'Number' using your figures.
- Complete the column headed 'Proportion of total', again using
your figures.
Look at the numbers in the boxes in Figure 1.
Along the top branches we have 29/100 and 23/29
In the 'Proportion of total' column we have 23/100.
Notice that: 29/100 x 23/29
= 23/100
- Look at the numbers you have put on the top branches of your tree
Do these multiply together to produce the first answer in your 'Proportion of total'
column? If so, write down the multiplication sum and answer.
- Look at the rest of Figure 1. Does the same connection work for any of the other
branches? If so, write them down.
- Look at the rest of your tree diagram. Does the same connection work for any other of
your proportions? If so, write them down.
Estimating Probabilities
If the results are collected for a large number of tests then the proportions thit are
obtained will tend to the PROBABLILTY something occurs.
For example, on the basis of our evidence we can estimate the probability that the
drunk driver reacts positively to the test is 23/29. The probability
that any driver is both drunk and reacts positively is estimated to be 23/100.
Make sure you understand the difference between these last two statements. Ask your
teacher for help if you don't understand.
Use the proportions in Figure 1 to estimate:
- the probability that a sober driver reacts positively to the test;
- the probability that any driver is both sober and reacts positively to the test;
- the probability that a driver is sober;
- the probability that a driver is both drunk and reacts positively to the test;
- the probability that a drunk driver reacts positively to the test;
- the probability that a driver is drunk.
Look at your answers to a, b, and c.
Two of the answers should multiply together to give the third.
- Write down these fractions as a multiplication sum with answer.
- Do the same for your answers to d, e, and f.
- Repeat questions a to h using the results obtained from your simulation.
Theoretical
Probabilities
The figures you have used were based on a sample of 100 random numbers. Proportions can
only be expected to approximate to the theoretical probabilities in the long run, which
means many more than 100 trials.
It would be from large numbers of triails that the percentages used in Section B2 were
obtained.
Look back at B2.
We assumed that 30% of the motorists on the road it this time were drunk.
We say that:
Probability (a motorist is drunk) = 30/100 = 3/10
We also say that:
Probability (a drunken motorist gives a positive reaction) = 80/100 =
8/10
Table 2 shows that. in the long run:
Probability (a motorist is both drunk and gives a positive reaction) = 24/100
But 3/10 x 8/10 =
24/100
Using the facts that:
3/10 = Probability (a motorist is drunk)
8/10 = Probability (a drunken motorist gives a positive reaction)
24/100 = Probability (a motorist is both drunk and gives a
positive reaction)
- Write the connection 3/10 x 8/10
= 24/100 in terms of probabilities, without using
numbers.
Use the percentages given in B2 to write down:
- Probability (a motorist is sober)
- Probability (a sober motorist gives a positive reaction)
Use Table 2 to help you find:
- Probability (a motorist is sober and gives a positive reaction).
- Write down the multiplication sum that connects the fractions in your answers to b, c
and d.
- Write the sum down in terms of probabilities, without using fractions.
|